1 Answer
Algorithms
They are following different formulas to compute Hamming windows
- In
R, it is
(25/46) – (21/46) * cos(2 * pi * (0:n)/N)
which can be viewed when typing hamming
> hamming
function (n, method = c("symmetric", "periodic"))
{
if (!isPosscal(n) || !isWhole(n) || n <= 0)
stop("n must be an integer strictly positive")
method <- match.arg(method)
if (method == "periodic") {
N <- n
}
else if (method == "symmetric") {
N <- n - 1
}
else {
stop("method must be either 'periodic' or 'symmetric'")
}
if (n == 1) {
w <- 1
}
else {
n <- n - 1
w <- (25/46) - (21/46) * cos(2 * pi * (0:n)/N)
}
w
}
- In
MATLAB, the algorithm is (see https://se.mathworks.com/help/signal/ref/hamming.html)
and there are some precision difference for two coefficients
> 25/46
[1] 0.5434783
> 21/46
[1] 0.4565217
Analysis
Two reasons that make the differences
- in
gsignals::hamming, if you choosesymmetricby default, you will haveN <- n-1andn <- n-1, that means the equivalent to Matlab’shammingshould behamming(76+1) - the approximations
0.54and0.46in Matlab contribute to the deviation from R’s version.
Tests with Handmade Implementations
We can implement hamming functions according to formulas from MATLAB and R, respectively, e.g.,
hamMatalb <- function(n) 0.54 - 0.46 * cos(2 * pi * (0:n) / n)
hamR <- function(n) 25 / 46 - 21 / 46 * cos(2 * pi * (0:n) / n)
and then run
> hamMatalb(75) # the same as obtained by hamming(76) in MATLAB
[1] 0.08000000 0.08161328 0.08644182 0.09445175 0.10558687 0.11976909
[7] 0.13689893 0.15685623 0.17950101 0.20467443 0.23219992 0.26188441
[13] 0.29351967 0.32688382 0.36174283 0.39785218 0.43495860 0.47280181
[19] 0.51111636 0.54963351 0.58808309 0.62619540 0.66370312 0.70034314
[25] 0.73585847 0.77000000 0.80252824 0.83321504 0.86184514 0.88821773
[31] 0.91214782 0.93346756 0.95202741 0.96769718 0.98036697 0.98994790
[37] 0.99637276 0.99959650 0.99959650 0.99637276 0.98994790 0.98036697
[43] 0.96769718 0.95202741 0.93346756 0.91214782 0.88821773 0.86184514
[49] 0.83321504 0.80252824 0.77000000 0.73585847 0.70034314 0.66370312
[55] 0.62619540 0.58808309 0.54963351 0.51111636 0.47280181 0.43495860
[61] 0.39785218 0.36174283 0.32688382 0.29351967 0.26188441 0.23219992
[67] 0.20467443 0.17950101 0.15685623 0.13689893 0.11976909 0.10558687
[73] 0.09445175 0.08644182 0.08161328 0.08000000
> hamR(75) # the same as obtained by gsignal::hamming(76) in R
[1] 0.08695652 0.08855761 0.09334964 0.10129899 0.11234992 0.12642490
[7] 0.14342521 0.16323161 0.18570516 0.21068824 0.23800559 0.26746562
[13] 0.29886168 0.33197355 0.36656897 0.40240529 0.43923112 0.47678818
[19] 0.51481302 0.55303893 0.59119778 0.62902190 0.66624601 0.70260898
[25] 0.73785576 0.77173913 0.80402141 0.83447617 0.86288979 0.88906296
[31] 0.91281211 0.93397064 0.95239015 0.96794144 0.98051542 0.99002390
[37] 0.99640019 0.99959955 0.99959955 0.99640019 0.99002390 0.98051542
[43] 0.96794144 0.95239015 0.93397064 0.91281211 0.88906296 0.86288979
[49] 0.83447617 0.80402141 0.77173913 0.73785576 0.70260898 0.66624601
[55] 0.62902190 0.59119778 0.55303893 0.51481302 0.47678818 0.43923112
[61] 0.40240529 0.36656897 0.33197355 0.29886168 0.26746562 0.23800559
[67] 0.21068824 0.18570516 0.16323161 0.14342521 0.12642490 0.11234992
[73] 0.10129899 0.09334964 0.08855761 0.08695652
and we can check the lengths of resulting windows
> length(hamMatalb(75))
[1] 76
> length(hamR(75))
[1] 76
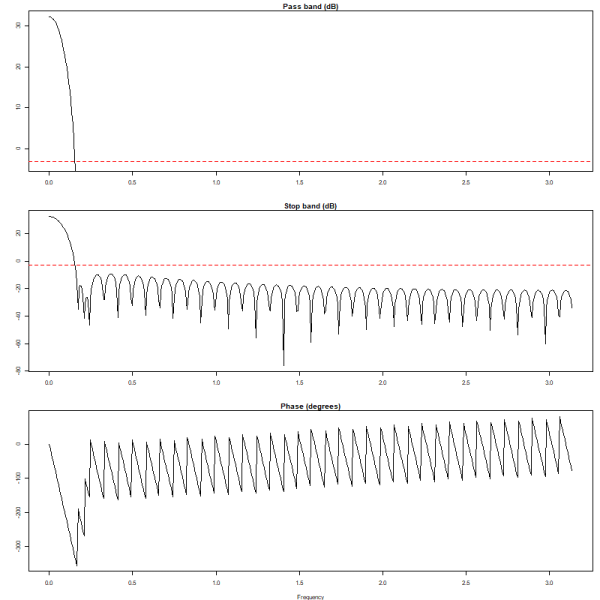
Spectral Performance
Given n <- 75, we can take a look at the difference in the frequency domain, using freqz. We can see that the difference mainly lies in the stopband but still quite minor, which doesn’t affect the filtering performance too much.
freqz(hamR(n))
freqz(hamMatlab(n))
9
-
3
+1, you beat me to this portion of the answer using the exact same links and nearly identical image of the algorithm. (I still think the core problem is that
gsignal::hamming(76)produces different numbers than the OP posted. Perhaps if you extended your example to manually calculate forn=76andn=77, it would provide a little more insight.)– r2evans
18 hours ago
-
More reference for context: en.wikipedia.org/wiki/Window_function#Hann_and_Hamming_windows says "Setting
a0to approximately 0.54, or more precisely 25/46, produces the Hamming window, proposed by Richard W. Hamming." This suggests Matlab is okay with approximating? (I'll duck whatever food fight that blasphemy incites 😉– r2evans
18 hours ago
-
1
@r2evans yes, from the source code of
gsignal::hamming,hamming(77)in R should be identical tohamming(76)in Matlab, but then the difference comes from the approximation.– ThomasIsCoding
18 hours ago
-
2
@SamR from the perspective of spectral analysis, it difference is negligible. You can see my latest update with spectral analysis.
– ThomasIsCoding
17 hours ago
-
2
@r2evans AFAIK, Hamming himself suggested the rounded numbers, I guess that is why MATLAB uses them. 25/46 is where the first side-lobe gets cancelled, the exact solution to Hamming’s constraint. Using 0.53836 instead one gets the lowest side-lobes, which is actually better. The rounded value sits in between these two solutions. But the difference between them is minor, and not noticeable if you are using 8 bits for your signal.
– Cris Luengo7 hours ago


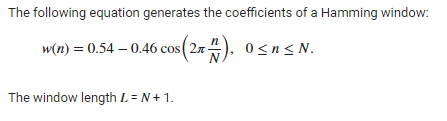

What package is
hammingfrom? It is not a base function. What function are you using in Matlab? Editing your question to explain in more detail what exactly you are doing may get you better, faster help – good luck!19 hours ago
in matlab
hammingis to design hamming windows for filters. What do you meanhammingin R?19 hours ago