I am wondering if there can be a version of Ackermann function with better time complexity than the standard variation.
This is not a homework and I am just curious. I know the Ackermann function doesn’t have any practical use besides as a performance benchmark, because of the deep recursion. I know the numbers grow very large very quickly, and I am not interested in computing it.
Even though I use Python 3 and the integers won’t overflow, I do have finite time, but I have implemented a version of it myself according to the definition found on Wikipedia, and computed the output for extremely small values, just to make sure the output is correct.
def A(m, n):
if not m:
return n + 1
return A(m - 1, A(m, n - 1)) if n else A(m - 1, 1)
The above code is a direct translation of the image, and is extremely slow, I don’t know how it can be optimized, is it impossible to optimize it?
One thing I can think of is to memoize it, but the recursion runs backwards, each time the function is recursively called the arguments were not encountered before, each successive function call the arguments decrease rather than increase, therefore each return value of the function needs to be calculated, memoization doesn’t help when you call the function with different arguments the first time.
Memoization can only help if you call it with the same arguments again, it won’t compute the results and will retrieve cached result instead, but if you call the function with any input with (m, n) >= (4, 2) it will crash the interpreter regardless.
I also implemented another version according to this answer:
def ack(x, y):
for i in range(x, 0, -1):
y = ack(i, y - 1) if y else 1
return y + 1
But it is actually slower:
In [2]: %timeit A(3, 4)
1.3 ms ± 9.75 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
In [3]: %timeit ack(3, 4)
2 ms ± 59.9 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Theoretically can Ackermann function be optimized? If not, can it be definitely proven that its time complexity cannot decrease?
I have just tested A(3, 9) and A(4, 1) will crash the interpreter, and the performance of the two functions for A(3, 8):
In [2]: %timeit A(3, 8)
432 ms ± 4.63 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
In [3]: %timeit ack(3, 8)
588 ms ± 10.4 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
I did some more experiments:
from collections import Counter
from functools import cache
c = Counter()
def A1(m, n):
c[(m, n)] += 1
if not m:
return n + 1
return A(m - 1, A(m, n - 1)) if n else A(m - 1, 1)
def test(m, n):
c.clear()
A1(m, n)
return c
The arguments indeed repeat.
But surprisingly caching doesn’t help at all:
In [9]: %timeit Ackermann = cache(A); Ackermann(3, 4)
1.3 ms ± 10.1 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Caching only helps when the function is called with the same arguments again, as explained:
In [14]: %timeit Ackermann(3, 2)
101 ns ± 0.47 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
I have tested it with different arguments numerous times, and it always gives the same efficiency boost (which is none).
7
6 Answers
6
Highest score (default)
Trending (recent votes count more)
Date modified (newest first)
Date created (oldest first)
Solution
I recently wrote a bunch of solutions based on the same paper that templatetypedef mentioned. Many use generators, one for each m-value, yielding the values for n=0, n=1, n=2, etc. This one might be my favorite:
def A_Stefan_generator_stack3(m, n):
def a(m):
if not m:
yield from count(1)
x = 1
for i, ai in enumerate(a(m-1)):
if i == x:
x = ai
yield x
return next(islice(a(m), n, None))
Explanation
Consider the generator a(m). It yields A(m,0), A(m,1), A(m,2), etc. The definition of A(m,n) uses A(m-1, A(m, n-1)). So a(m) at its index n yields A(m,n), computed like this:
- A(m,n-1) gets yielded by the
a(m)generator itself at index n-1. Which is just the previous value (x) yielded by this generator. - A(m-1, A(m, n-1)) = A(m-1, x) gets yielded by the
a(m-1)generator at index x. So thea(m)generator iterates over thea(m-1)generator and grabs the value at index i == x.
Benchmark
Here are times for computing all A(m,n) for m≤3 and n≤17, also including templatetypedef’s solution:
1325 ms A_Stefan_row_class
1228 ms A_Stefan_row_lists
544 ms A_Stefan_generators
1363 ms A_Stefan_paper
459 ms A_Stefan_generators_2
866 ms A_Stefan_m_recursion
704 ms A_Stefan_function_stack
468 ms A_Stefan_generator_stack
945 ms A_Stefan_generator_stack2
582 ms A_Stefan_generator_stack3
467 ms A_Stefan_generator_stack4
1652 ms A_templatetypedef
Code
def A_Stefan_row_class(m, n):
class A0:
def __getitem__(self, n):
return n + 1
class A:
def __init__(self, a):
self.a = a
self.n = 0
self.value = a[1]
def __getitem__(self, n):
while self.n < n:
self.value = self.a[self.value]
self.n += 1
return self.value
a = A0()
for _ in range(m):
a = A(a)
return a[n]
from collections import defaultdict
def A_Stefan_row_lists(m, n):
memo = defaultdict(list)
def a(m, n):
if not m:
return n + 1
if m not in memo:
memo[m] = [a(m-1, 1)]
Am = memo[m]
while len(Am) <= n:
Am.append(a(m-1, Am[-1]))
return Am[n]
return a(m, n)
from itertools import count
def A_Stefan_generators(m, n):
a = count(1)
def up(a, x=1):
for i, ai in enumerate(a):
if i == x:
x = ai
yield x
for _ in range(m):
a = up(a)
return next(up(a, n))
def A_Stefan_paper(m, n):
next = [0] * (m + 1)
goal = [1] * m + [-1]
while True:
value = next[0] + 1
transferring = True
i = 0
while transferring:
if next[i] == goal[i]:
goal[i] = value
else:
transferring = False
next[i] += 1
i += 1
if next[m] == n + 1:
return value
def A_Stefan_generators_2(m, n):
def a0():
n = yield
while True:
n = yield n + 1
def up(a):
next(a)
a = a.send
i, x = -1, 1
n = yield
while True:
while i < n:
x = a(x)
i += 1
n = yield x
a = a0()
for _ in range(m):
a = up(a)
next(a)
return a.send(n)
def A_Stefan_m_recursion(m, n):
ix = [None] + [(-1, 1)] * m
def a(m, n):
if not m:
return n + 1
i, x = ix[m]
while i < n:
x = a(m-1, x)
i += 1
ix[m] = i, x
return x
return a(m, n)
def A_Stefan_function_stack(m, n):
def a(n):
return n + 1
for _ in range(m):
def a(n, a=a, ix=[-1, 1]):
i, x = ix
while i < n:
x = a(x)
i += 1
ix[:] = i, x
return x
return a(n)
from itertools import count, islice
def A_Stefan_generator_stack(m, n):
a = count(1)
for _ in range(m):
a = (
x
for a, x in [(a, 1)]
for i, ai in enumerate(a)
if i == x
for x in [ai]
)
return next(islice(a, n, None))
from itertools import count, islice
def A_Stefan_generator_stack2(m, n):
a = count(1)
def up(a):
i, x = 0, 1
while True:
i, x = x+1, next(islice(a, x-i, None))
yield x
for _ in range(m):
a = up(a)
return next(islice(a, n, None))
def A_Stefan_generator_stack3(m, n):
def a(m):
if not m:
yield from count(1)
x = 1
for i, ai in enumerate(a(m-1)):
if i == x:
x = ai
yield x
return next(islice(a(m), n, None))
def A_Stefan_generator_stack4(m, n):
def a(m):
if not m:
return count(1)
return (
x
for x in [1]
for i, ai in enumerate(a(m-1))
if i == x
for x in [ai]
)
return next(islice(a(m), n, None))
def A_templatetypedef(i, n):
positions = [-1] * (i + 1)
values = [0] + [1] * i
while positions[i] != n:
values[0] += 1
positions[0] += 1
j = 1
while j <= i and positions[j - 1] == values[j]:
values[j] = values[j - 1]
positions[j] += 1
j += 1
return values[i]
funcs = [
A_Stefan_row_class,
A_Stefan_row_lists,
A_Stefan_generators,
A_Stefan_paper,
A_Stefan_generators_2,
A_Stefan_m_recursion,
A_Stefan_function_stack,
A_Stefan_generator_stack,
A_Stefan_generator_stack2,
A_Stefan_generator_stack3,
A_Stefan_generator_stack4,
A_templatetypedef,
]
N = 18
args = (
[(0, n) for n in range(N)] +
[(1, n) for n in range(N)] +
[(2, n) for n in range(N)] +
[(3, n) for n in range(N)]
)
from time import time
def print(*args, print=print, file=open('out.txt', 'w')):
print(*args)
print(*args, file=file, flush=True)
expect = none = object()
for _ in range(3):
for f in funcs:
t = time()
result = [f(m, n) for m, n in args]
# print(f'{(time()-t) * 1e3 :5.1f} ms ', f.__name__)
print(f'{(time()-t) * 1e3 :5.0f} ms ', f.__name__)
if expect is none:
expect = result
elif result != expect:
raise Exception(f'{f.__name__} failed')
del result
print()
5
-
1
A thought on how to improve this: we know that A(1, n) = 2n + 3 for all n. Perhaps you can eliminate the last two levels of the recursion by directly returning 2n+3 whenever A(1, n) is requested?
– templatetypedef9 hours ago
-
@templatetypedef Well, yes, and there are similar formulas for m=2 and m=3, and a simple faster calculation for m=4. So we could optimize a few more levels with that. I personally wasn't interested in that math solution. I was actually preparing a question+answer about this myself, ruling out such math solutions in the question. It was going to be about coding techniques, about avoiding deep recursion and avoiding recalculation. Skipping values with math insights was going to be ruled out. Somehow I thought this question also wanted that, but I see now that I misread it. Oh well 🙂
– Stefan Pochmann9 hours ago
-
@templatetypedef Hmm, that said, while the formulas for small m are boring, the ones for larger m, using arrow notation, might be interesting. They're shown in the table of values on Wikipedia. There's even A(m,n) = (2 → (n+3) → (m-2)) – 3, but I don't remember what the arrow notation means. Might be fun to implement that.
– Stefan Pochmann8 hours ago
-
Also… any idea why my implementation is so slow? I’m surprised that it was the worst of the bunch. 🙂
– templatetypedef6 hours ago
-
@templatetypedef: Your implementation is slow because you did memoization (
cache(...)) incorrectly, see Kelly Bundy's answer. Other reasons for the slowness can be that other implementations are extremely smart.– pts6 hours ago
v0 is pretty much your code:
def ack(m, n):
if m == 0: return n + 1
return ack(m - 1, 1) if n == 0 else ack(m - 1, ack(m, n - 1))
This calculates ack(3, 9) in 2.49s. ack() is called 11164370 times. Surely we can cache the values already calculated saving tonns of calls to the function.
v1 uses a dict for a cache and only calculates if the result is not in the cache:
c = {}
def ack(m, n):
global c
if "{}-{}".format(m, n) in c: return c["{}-{}".format(m, n)]
else:
if m == 0: ret = n + 1
else: ret = ack(m - 1, 1) if n == 0 else ack(m - 1, ack(m, n - 1))
c["{}-{}".format(m, n)] = ret
return ret
This calculates ack(3, 9) in 0.03s and with that ack(3, 9) is no longer suitable for measuring execution time. This time ack() is called 12294 times, the saving is enormous. But we can do it better. From now on we use ack(3, 13) that currently runs for 0.23s.
v2 only cares for caching where m > 0, since the case of m == 0 is trivial. With that space complexity is somewhat reduced:
c = {}
def ack(m, n):
global c
if m == 0: return n + 1
else:
if "{}-{}".format(m, n) in c: return c["{}-{}".format(m, n)]
else: ret = ack(m - 1, 1) if n == 0 else ack(m - 1, ack(m, n - 1))
c["{}-{}".format(m, n)] = ret
return ret
This finishes ack(3, 13) in 0.18s. But we can to even better.
v3 saves a bit of time by calculating the key in the cache only once per iteration:
c = {}
def ack(m, n):
global c
if m == 0: return n + 1
else:
key = "{}-{}".format(m, n)
if key in c: return c[key]
else: ret = ack(m - 1, 1) if n == 0 else ack(m - 1, ack(m, n - 1))
c[key] = ret
return ret
This time it runs for 0.14s. I surely can’t do much more to it around midnight but I will think about it some more. Ez jó mulatság, férfi munka volt – for those who know what that means.
2
-
1
You can use tuples as dictionary keys.
– MatBailie13 hours ago
-
1
Sure, I don't really program in Python, only for DIY purposes like this. I'm sure the pros can take it a bit further. I might have another look at it tomorrow. The problem is that running it guts out my laptop. ack(3, 14) explodes even with max recursion set to 200000, yet it finishes in 0.14s 😀
– Gambanishu Habbeba13 hours ago
But surprisingly caching doesn’t help at all:
In [9]: %timeit Ackermann = cache(A); Ackermann(3, 4) 1.3 ms ± 10.1 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
That’s because you did that wrong. Only your Ackermann is memoized, not your A. And the recursive calls all go to A.
Times for m,n = 3,8, including a properly memoized version B:
440.30 ms A(m, n)
431.11 ms Ackermann = cache(A); Ackermann(m, n)
1.74 ms B.cache_clear(); B(m, n)
About B:
- Print
B.cache_info())afterwards to see how well the cache did:CacheInfo(hits=1029, misses=5119, maxsize=None, currsize=5119). SoBhad 5,119 "real" calls (where it had to do work) and 1,029 calls that were answered from cache. Without the memoization, it gets called 2,785,999 times. - For m,n = 3,12 it takes ~32 ms.
- For m,n = 3,13 it crashes due to the deep recursion.
Code:
from timeit import repeat
import sys
sys.setrecursionlimit(999999)
setup = '''
from functools import cache
def A(m, n):
if not m:
return n + 1
return A(m - 1, A(m, n - 1)) if n else A(m - 1, 1)
@cache
def B(m, n):
if not m:
return n + 1
return B(m - 1, B(m, n - 1)) if n else B(m - 1, 1)
m, n = 3, 8
'''
codes = [
'A(m, n)',
'Ackermann = cache(A); Ackermann(m, n)',
'B.cache_clear(); B(m, n)',
]
for code in codes:
t = min(repeat(code, setup, number=1))
print(f'{t*1e3:6.2f} ms ', code)
Here’s my stab at a Python implementation of the Grossman-Zeitman algorithm, which iteratively computes A(i, n) in O(A(i, n)) time. For a description of how this algorithm works, check the linked question.
def ackermann(i, n):
positions = [-1] * (i + 1)
values = [0] + [1] * i
while positions[i] != n:
values[0] += 1
positions[0] += 1
j = 1
while j <= i and positions[j - 1] == values[j]:
values[j] = values[j - 1]
positions[j] += 1
j += 1
return values[i]
Given that the inner loop is very tight and there’s no recursion, I suspect this will likely outperform the basic recursive solution you initially posted. However, I haven’t correctness- or time-tested this implementation; it’s based on the Java code I wrote in the linked question.
0
TL;DR The Ackermann function grows so rapidly that for (m >= 4 and n >= 3) the result won’t fit to RAM. For smaller values of m or n, it’s very easy to compute the values directly (without recursion) and quickly.
I know that this answer doesn’t help optimizing recursive function calls, nevertheless it provides a fast solution (with analysis) for computing values of the Ackermann function on real, contemporary computers, and it provides a direct answer to the first paragraph of the question.
We want to store the result in an unsigned binary big integer variable on a
computer. To store the value 2 ** b, we need (b + 1) bits of data, and (c1 + c2 * ceil(log2(b))) bits of header for storing the length b itself. (c1 is a
nonnegative integer, c2 is a positive integer.) Thus we need more than b
bits of RAM to store 2 ** b.
Computers with huge amounts of RAM:
- In 2023 consumer-grade PCs have up to 128 GiB of RAM, and there are commercially
available servers with 2 TiB of RAM
(https://ramforyou.com/is-it-possible-for-a-computer-have-1tb-ram). - In 2020, a single-rack server with 6 TiB of RAM was built
(https://www.youtube.com/watch?v=uHAfTty9UWY). - In 2017, a large server with 160 TiB of RAM was constructed
(https://www.forbes.com/sites/aarontilley/2017/05/16/hpe-160-terabytes-memory/). - So we can say that in 2023 it’s not feasible to build a computer with 1
PiB == 1024 TiB of RAM, and 1 EiB == 1024 PiB == 1048576 TiB == (2 ** 63)
bits is completely impossible in 2023 and the near future. - The current estimate for the number of atoms in the universe is 10 ** 82
== 10 * 10 ** 81 < 16 * 2 ** 270 < 2 ** 274. - Let’s imagine the biggest computer. Even if there are many more atoms, say
2 ** 300, and we can use all of them in a single computer, and we can
store 1 EiB of data in a single atom, thus we have 2 ** 363 bits of
memory; that’s still too small to store the Big value 2 ** (2 ** 363).
Let’s see which of Knuth’s up-arrow notation
(https://en.wikipedia.org/wiki/Knuth%27s_up-arrow_notation) values are less
than Big:
-
2 ^ b == 2 ** b: It works for 1 <= b <= (2 ** 363 – 1).
2 ^ (2 ** 363) == 2 ** (2 ** 363) == Big >= Big.
-
2 ^^ b: It works for 1 <= b <= 5.
2 ^^ 1 == 2;
2 ^^ 2 == 2 ** 2 == 4;
2 ^^ 3 == 2 ** (2 ** 2) == 16;
2 ^^ 4 == 2 ** (2 ** (2 ** 2)) == 65536;
2 ^^ 5 == 2 ** (2 ** (2 ** (2 ** 2))) == 2 ** 65536 == 2 ** (2 ** 16) < Big;
2 ^^ 6 == 2 ** (2 ** (2 ** (2 ** (2 ** 2)))) == 2 ** (2 ** 65536) >= Big.
-
2 ^^^ b: It works for 1 <= b <= 3.
2 ^^^ 1 == 2;
2 ^^^ 2 == 2 ^^ 2 == 4;
2 ^^^ 3 == 2 ^^ (2 ^^ 2) == 65536;
2 ^^^ 4 == 2 ^^ (2 ^^ (2 ^^ 2)) == 2 ^^ 65536 >= 2 ^^ 6 >= Big.
-
2 ^^^^ b: It works for 1 <= b <= 2.
2 ^^^^ 1 == 2;
2 ^^^^ 2 == 2 ^^^ 2 == 4;
2 ^^^^ 3 == 2 ^^^ (2 ^^^ 2) == 2 ^^^ 4 == 2 ^^ 65536 >= 2 ^^ 6 >= Big.
-
2 ^^^^^ b and even more arrows: It works for 1 <= b <= 2. The value is at
least 2 ^^^^ b, see there.
Thus here is how to compute the feasible values in Python:
def up_arrow(a, b):
if b <= 2:
if b < 0:
raise ValueError
return (1, 2, 4)[b]
elif a == 1:
if b >> 363:
raise ValueError
return 1 << b # This may run out of memory for large b.
elif a == 2:
if b > 5:
raise ValueError
if b == 5:
return 1 << 65536
return (16, 65536)[b - 3]
elif a == 3:
if b > 3:
raise ValueError
return 65536
else:
raise ValueError
Given that for m >= 3, ack(m, n) == up_arrow(m – 2, n + 3) – 3
(see also https://en.wikipedia.org/wiki/Ackermann_function#Table_of_values),
we can compute the feasible values of the Ackermann function:
def ack(m, n):
if n < 0:
raise ValueError
if m in (0, 1):
return n + (m + 1) # This may run out of memory for large n.
elif m == 2:
return (n << 1) + 3 # This may run out of memory for large n.
elif m == 3:
if n >> 360:
raise ValueError
return (1 << (n + 3)) - 3 # This may run out of memory for large n.
elif m == 4:
if n > 2:
raise ValueError
if n == 2:
return (1 << 65536) - 3
return (13, 65533)[n]
elif m == 5:
if n > 0:
raise ValueError
return 65533
else:
raise ValueError
print([ack(m, 0) for m in range(6)])
print([ack(m, 1) for m in range(5)])
print([ack(m, 2) for m in range(5)])
print([ack(m, 3) for m in range(4)])
print([ack(m, 4) for m in range(4)])
The question has tag Python, but using ctypes to call C++ code is also a Python feature. It’s ~20000x faster than the top Python answer. Or ~13-15x faster if you don’t use math optimization for special cases. There’s a direct math solution for each m, but I assume you want a recursive-like solution.
Time cost to calculate Ackermann number for all pairs m <= 3, n <= 17:
- Use math: ~20 microsecond
- Not use math: ~30 ms
// ackermann.cpp
#include <iostream>
#include <vector>
#include <chrono>
using namespace std;
class MyTimer {
std::chrono::time_point<std::chrono::system_clock> start;
public:
void startCounter() {
start = std::chrono::system_clock::now();
}
int64_t getCounterNs() {
return std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now() - start).count();
}
int64_t getCounterMs() {
return std::chrono::duration_cast<std::chrono::milliseconds>(std::chrono::system_clock::now() - start).count();
}
double getCounterMsPrecise() {
return std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now() - start).count()
/ 1000000.0;
}
};
extern "C" {
int64_t ackermann(int64_t m, int64_t n) {
static std::vector<int64_t> cache[4];
// special signal to clear cache
if (m < 0 && n < 0) {
for (int i = 0; i < 4; i++) {
cache[i].resize(0);
cache[i].shrink_to_fit();
}
return -1;
}
if (n >= cache[m].size()) {
int cur = cache[m].size();
cache[m].resize(n + 1);
for (int i = cur; i < n; i++) cache[m][i] = ackermann(m, i);
}
if (cache[m][n]) return cache[m][n];
if (m == 0) return cache[m][n] = n + 1;
// These 3 lines are kinda cheating, since it uses math formula for special case
// Comment them out in case you dont want to use that.
if (m == 1) return cache[m][n] = n + 2;
if (m == 2) return cache[m][n] = 2 * n + 3;
if (m == 3) return cache[m][n] = (1LL << (n + 3)) - 3;
if (n == 0) return cache[m][n] = ackermann(m - 1, 1);
return cache[m][n] = ackermann(m - 1, ackermann(m, n - 1));
}
}
volatile int64_t dummy = 0;
int main()
{
MyTimer timer;
timer.startCounter();
for (int m = 0; m <= 3; m++)
for (int n = 0; n <= 17; n++) {
dummy = ackermann(m, n);
// cout << "ackermann(" << m << ", " << n << ") = " << dummy << "n";
}
cout << "ackermann cost = " << timer.getCounterMsPrecise() << "n";
}
Compile the above using g++ ackermann.cpp -shared -fPIC -O3 -std=c++17 -o ackermann.so
To run separately, use
g++ -o main_cpp ackermann.cpp -O3 -std=c++17
./main_cpp
Then in the same folder, run this script (modified from @Stefan Pochmann answer)
def A_Stefan_row_class(m, n):
class A0:
def __getitem__(self, n):
return n + 1
class A:
def __init__(self, a):
self.a = a
self.n = 0
self.value = a[1]
def __getitem__(self, n):
while self.n < n:
self.value = self.a[self.value]
self.n += 1
return self.value
a = A0()
for _ in range(m):
a = A(a)
return a[n]
from collections import defaultdict
def A_Stefan_row_lists(m, n):
memo = defaultdict(list)
def a(m, n):
if not m:
return n + 1
if m not in memo:
memo[m] = [a(m-1, 1)]
Am = memo[m]
while len(Am) <= n:
Am.append(a(m-1, Am[-1]))
return Am[n]
return a(m, n)
from itertools import count
def A_Stefan_generators(m, n):
a = count(1)
def up(a, x=1):
for i, ai in enumerate(a):
if i == x:
x = ai
yield x
for _ in range(m):
a = up(a)
return next(up(a, n))
def A_Stefan_paper(m, n):
next = [0] * (m + 1)
goal = [1] * m + [-1]
while True:
value = next[0] + 1
transferring = True
i = 0
while transferring:
if next[i] == goal[i]:
goal[i] = value
else:
transferring = False
next[i] += 1
i += 1
if next[m] == n + 1:
return value
def A_Stefan_generators_2(m, n):
def a0():
n = yield
while True:
n = yield n + 1
def up(a):
next(a)
a = a.send
i, x = -1, 1
n = yield
while True:
while i < n:
x = a(x)
i += 1
n = yield x
a = a0()
for _ in range(m):
a = up(a)
next(a)
return a.send(n)
def A_Stefan_m_recursion(m, n):
ix = [None] + [(-1, 1)] * m
def a(m, n):
if not m:
return n + 1
i, x = ix[m]
while i < n:
x = a(m-1, x)
i += 1
ix[m] = i, x
return x
return a(m, n)
def A_Stefan_function_stack(m, n):
def a(n):
return n + 1
for _ in range(m):
def a(n, a=a, ix=[-1, 1]):
i, x = ix
while i < n:
x = a(x)
i += 1
ix[:] = i, x
return x
return a(n)
from itertools import count, islice
def A_Stefan_generator_stack(m, n):
a = count(1)
for _ in range(m):
a = (
x
for a, x in [(a, 1)]
for i, ai in enumerate(a)
if i == x
for x in [ai]
)
return next(islice(a, n, None))
from itertools import count, islice
def A_Stefan_generator_stack2(m, n):
a = count(1)
def up(a):
i, x = 0, 1
while True:
i, x = x+1, next(islice(a, x-i, None))
yield x
for _ in range(m):
a = up(a)
return next(islice(a, n, None))
def A_Stefan_generator_stack3(m, n):
def a(m):
if not m:
yield from count(1)
x = 1
for i, ai in enumerate(a(m-1)):
if i == x:
x = ai
yield x
return next(islice(a(m), n, None))
def A_Stefan_generator_stack4(m, n):
def a(m):
if not m:
return count(1)
return (
x
for x in [1]
for i, ai in enumerate(a(m-1))
if i == x
for x in [ai]
)
return next(islice(a(m), n, None))
def A_templatetypedef(i, n):
positions = [-1] * (i + 1)
values = [0] + [1] * i
while positions[i] != n:
values[0] += 1
positions[0] += 1
j = 1
while j <= i and positions[j - 1] == values[j]:
values[j] = values[j - 1]
positions[j] += 1
j += 1
return values[i]
import ctypes
mylib = ctypes.CDLL('./ackermann.so')
mylib.ackermann.argtypes = [ctypes.c_int64, ctypes.c_int64]
mylib.ackermann.restype = ctypes.c_int64
def c_ackermann(m, n):
return mylib.ackermann(m,n)
funcs = [
c_ackermann,
A_Stefan_row_class,
A_Stefan_row_lists,
A_Stefan_generators,
A_Stefan_paper,
A_Stefan_generators_2,
A_Stefan_m_recursion,
A_Stefan_function_stack,
A_Stefan_generator_stack,
A_Stefan_generator_stack2,
A_Stefan_generator_stack3,
A_Stefan_generator_stack4,
A_templatetypedef
]
N = 18
args = (
[(0, n) for n in range(N)] +
[(1, n) for n in range(N)] +
[(2, n) for n in range(N)] +
[(3, n) for n in range(N)]
)
from time import time
def print(*args, print=print, file=open('out.txt', 'w')):
print(*args)
print(*args, file=file, flush=True)
expect = none = object()
for _ in range(3):
for f in funcs:
t = time()
result = [f(m, n) for m, n in args]
# print(f'{(time()-t) * 1e3 :5.1f} ms ', f.__name__)
print(f'{(time()-t) * 1e3 :5.0f} ms ', f.__name__)
if expect is none:
expect = result
elif result != expect:
raise Exception(f'{f.__name__} failed')
del result
print()
c_ackermann(-1, -1)
Output:
0 ms c_ackermann
1897 ms A_Stefan_row_class
1427 ms A_Stefan_row_lists
437 ms A_Stefan_generators
1366 ms A_Stefan_paper
479 ms A_Stefan_generators_2
801 ms A_Stefan_m_recursion
725 ms A_Stefan_function_stack
716 ms A_Stefan_generator_stack
1113 ms A_Stefan_generator_stack2
551 ms A_Stefan_generator_stack3
682 ms A_Stefan_generator_stack4
1622 ms A_templatetypedef
Your Answer
Post as a guest
Required, but never shown
Post as a guest
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.
Not the answer you're looking for? Browse other questions tagged
or ask your own question.
or ask your own question.
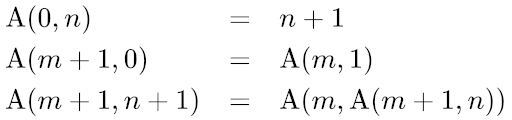







This question might be more suitable for cs.stackexchange.com or cstheory.stackexchange.com Guessing by a quick Google Scholar search the implementation of the Ackermann function can be optimized, e.g. sciencedirect.com/science/article/pii/0304397588900461 (1988) or dl.acm.org/doi/abs/10.1145/966049.777398 (2003)
17 hours ago
I don't think there's much you can do outside of cheating and simply using a hardcoded lookup table for small values of m and n and erroring for larger values.
17 hours ago
According to the Wikipedia page that you mentioned, you cannot avoid a huge time complexity. However, depending of the algorithm, you may have or not a huge space complexity. And a huge space complexity may crash your program.
17 hours ago
Memoization totally helps time complexity. Just put a simple
print(m, n)a the beginning and callA(3, 2). You will see repeated values over and over. E.g. A(1, 5) is called 16 times. Caching will most definitely make it faster.17 hours ago
This earlier question explores a fast iterative algorithm for computing Ackermann values. I haven’t benchmarked it but perhaps it fits your needs? (It’s also asymptotically faster than the naive recursion.)
15 hours ago
|
Show 2 more comments